Základní síťové teorémy používané v síťové analýze jsou k dispozici v různých typech, jako je Thévenin, superpozice, Norton, substituce, maximální přenos energie, reciprocita a Millmanovy věty . Každý teorém má své vlastní aplikační oblasti. Pochopení každého síťového teorému je tedy velmi důležité, protože tyto teorémy lze opakovaně používat v různých obvodech. Tyto věty nám pomáhají při řešení složitých síťových obvodů pro danou podmínku. Tento článek pojednává o jednom z typů věty o síti substituční věta – příklady.
Co je substituční teorém?
Výrok substituční věty je; že kdykoli je známý proud v celé větvi nebo napětí v jakékoli větvi v síti, pak lze větev změnit kombinací různých prvků, které vytvoří podobné napětí a proud v celé větvi. Jinými slovy, může být definován jako; pro ekvivalenci větve by tepelné napětí i proud měly být shodné.
Koncept substituční věty závisí především na substituci jednoho prvku jiným prvkem. Tato věta je také velmi užitečná při dokazování některých dalších vět. Ačkoli tato věta není použitelná pro řešení věty, která zahrnuje výše uvedené dva zdroje, které nejsou zapojeny ani sériově, ani paralelně.
Vysvětlení substituční věty
Kroky spojené s řešením substituční věty zahrnují především následující.
Krok 1: Nejprve musíme najít napětí a proud všech prvků sítě. Obecně lze napětí a proud vypočítat pomocí ohmského zákona, Kirchoffovy zákony jako KVL nebo KCL.
Krok 2: Vyberte požadovanou větev, kterou chcete odstranit, prostřednictvím jiného prvku, jako je zdroj napětí/odpor a zdroj proudu.
Krok 3: Najděte správnou hodnotu nahrazeného prvku za předpokladu, že by se napětí a proud neměly měnit.
Krok 4: Zkontrolujte nový obvod jednoduchým výpočtem proudu a napětí všech prvků a vyhodnoťte jej původní sítí.
Schéma obvodu substituční věty
Pomocí následujícího schématu zapojení snadno pochopíme substituční teorém. Víme, že substituční teorém je nahrazením jednoho prvku jiným ekvivalentním prvkem. Pokud je jakýkoli prvek v síti nahrazen/nahrazen zdrojem proudu nebo zdrojem napětí, jehož proud a napětí v prvku nebo napříč prvkem zůstanou nezměněny jako u předchozí sítě.
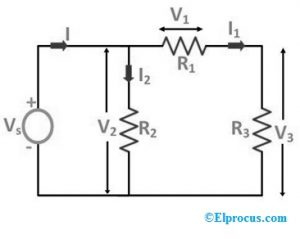
Různé odpory jako R1, R2 a R3 jsou připojeny jednoduše přes zdroj napětí. Proud proudu „I“ protékající obvodem je rozdělen na I1 a I2, kde „I1“ je přiváděn skrz odpor „R1“ a „I2“ protéká odporem R2, jak je znázorněno v obvodu. Zde jsou poklesy napětí na odporech R1, R2 a R3 odpovídajícím způsobem V1, V2 a V3.
Nyní, pokud je odpor „R3“ nahrazen zdrojem napětí „V3“, jak je znázorněno na následujícím schématu zapojení níže:
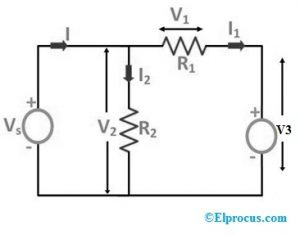
V následujícím schématu zapojení je odpor „R3“ nahrazen tokem proudu skrz tento prvek „I1“.
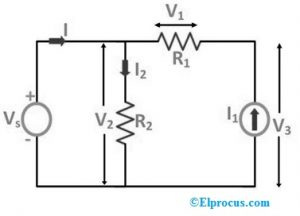
Z výše uvedených dvou případů, pokud je prvek nahrazen zdrojem proudu nebo napětí, pak se počáteční podmínky obvodu nemění, to znamená, že napájecí napětí přes odpor a zdroj proudu v celém odporu se nezmění, i když jsou nahrazeny jiným prameny.
Příklady problémů
Příklady příkladů substituční věty jsou diskutovány níže.
Příklad1:
Vyřešte následující obvod pomocí substituční věty pro výpočet napětí a proudu ve všech rezistorech.
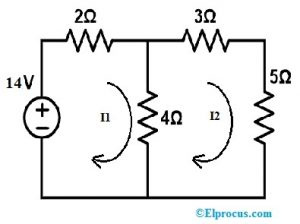
Krok 1:
Nejprve použijte KVL na smyčku1 ve výše uvedeném obvodu
14 = 6I1 – 4I2 ….(1)
Aplikujte KVL na smyčku 2 ve výše uvedeném obvodu
0 = 12I2 – 4I1
12 I2 = 4I1 => I1 = 3I2……….(2)
Dosaďte tuto rovnici 2 do výše uvedené rovnice 1.
14 = 6(3I2)-4I2
14 = 18I2 – 4I2 =>14I2 => 1A
I2 = 1A
Z výše uvedené rovnice-(2)
I1 = 3I2
Víme, že I2 = 1A
I1 = 3A
Krok 2:
V tomto kroku musíme odstranit větve loop1, abychom vytvořili jedinou smyčku.
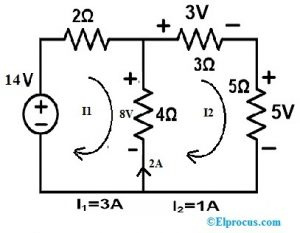
Krok 3:
Na místo rezistoru 4Ω můžeme umístit zdroj proudu/zdroj napětí. Nyní použijeme zdroj proudu.
Tok proudu smyčkou2 v obvodu je 1A. Nahradíme tedy větev zdrojem proudu 1A. V důsledku toho je zbytkový obvod zobrazen níže.
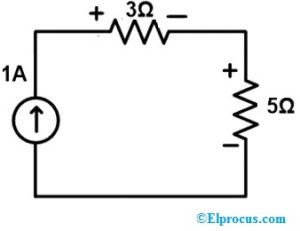
Krok 4:
V tomto kroku je třeba zkontrolovat napětí a proud všech prvků. Výše uvedený obvod obsahuje jedinou smyčku, tj. zdroj proudu. Hodnota protékajícího proudu smyčkou je tedy podobná hodnotě zdroje proudu.
Zde je aktuální hodnota zdroje 1A. Takže tok proudu skrz 3Ω a 5Ω odporové větve je 1A, což je podobné původní síti.
Pomocí ohmův zákon , zjistěte hodnotu napětí na rezistoru 3Ω
V = IS
V = I x R
V = 1 x 3 => 3V.
Podobně pomocí ohmového zákona musíme najít hodnotu napětí na odporu 5Ω.
V = IS
V = I x 5
V = 1 x 5 => 5V.
Proud a napětí jsou tedy podobné původní síti. Takže takto funguje tato věta.
Nyní, když v kroku 3 zvolíme zdroj napětí místo zdroje proudu. Takže v tomto stavu je hodnota zdroje napětí podobná hodnotě větve 4Ω rezistoru.
Tok proudu skrz 4Ω odporovou větev v rámci původní sítě je
I1 – I2 => 3 – 1 => 2A
Podle Ohmova zákona;
Napětí na rezistoru 4Ω je V = 2 x 4 = 8V
Potřebujeme tedy zapojit zdroj napětí s 8V do sítě a zbytkový obvod je znázorněn na níže uvedeném schématu.
V= 2 x 4 = 8V
Potřebujeme tedy připojit 8V zdroj napětí k síti a zbývající obvod je takový, jak je znázorněno na obrázku níže.
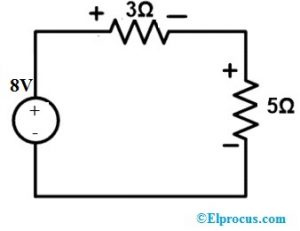
Aplikujte KVL na výše uvedenou smyčku, abyste ověřili napětí a proud.
8 = 3I + 5I => 8I
I = 1A.
Pomocí ohmského zákona lze napětí na rezistoru 3Ω vypočítat jako;
V = 1 × 3 => 3V
Podobně je napětí na rezistoru 5Ω;
V= 1 × 5 => 5V
Napětí a proud jsou tedy po nahrazení stejné jako u původní sítě.
Příklad2:
Vezměme následující obvod, abychom použili substituční teorém.
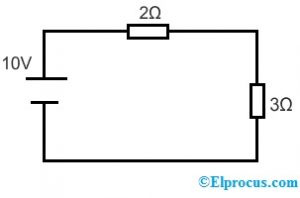
Podle pravítka dělení napětí je napětí na rezistorech 2Ω & 3Ω;
Napětí na rezistoru 3Ω je
V = 10×3/3+2 = 6V
Napětí na rezistoru 2Ω je
V = 10×2/3+2 = 4V
Tok proudu v obvodu se vypočítá jako I = 10/3+2 = 2A.
Pokud ve výše uvedeném obvodu nahradíme 6V zdroj napětí místo odporu 3Ω, obvod bude vypadat následovně.
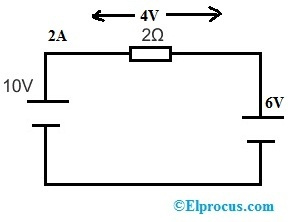
Na základě Ohmova zákona je napětí na odporu 2Ω a tok proudu v obvodu je
V = 10-6 => 4V
I = 10-6/2 = 2A
Pokud místo rezistoru 3Ω nahradíme zdroj proudu 2A, obvod bude vypadat následovně.
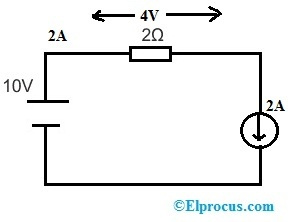
Napětí na odporu 2Ω je V = 10 – 3* 2 => 4 V & napětí na zdroji proudu ‚2A‘ je V = 10 – 4 => 6 V. Napětí na odporu 2Ω a proud v obvodu se tedy nezmění.
Výhody
The výhody substituční věty zahrnout následující.
- Tento koncept věty závisí hlavně na substituci jednoho prvku jiným prvkem.
- Tento teorém poskytuje intuici o chování obvodu a také pomáhá při ověřování různých dalších síťových teorémů.
- Výhodou použití této věty je, že tato věta poskytuje správné hodnoty pro proměnné jako X & Y, které odpovídají průsečíku.
Omezení
The omezení substituční věty zahrnout následující.
- Tuto větu nelze použít pro řešení sítě, která obsahuje minimálně dva nebo více zdrojů, které nejsou v rámci série/paralelní.
- V této větě by se při výměně prvku nemělo chování obvodu změnit.
Aplikace
The aplikace substituční věty zahrnout následující.
- Substituční teorém se používá k prokázání mnoha dalších teorémů.
- Tato věta je užitečná při řešení soustavy rovnic v matematice.
- Tato věta nahrazuje jeden prvek obvodu jedním dalším prvkem.
- Tato věta se používá k analýze obvodů se závislými zdroji.
Na kterém obvodu neplatí substituční teorém?
Obvod, který má výše uvedené dva zdroje, které jsou zapojeny buď paralelně nebo sériově, pak tato věta o substituci není použitelná.
Proč se kompenzační věta nazývá substituce?
Obě věty jako kompenzace a substituce jsou z hlediska procedury a redukce totožné. Tato věta je tedy použitelná pro antény a nazývá se také věta o substituci.
Jak používáte substituční teorém?
Tuto větu lze použít nahrazením libovolné větve jinou větví v rámci sítě, aniž by došlo k narušení napětí a proudů v celé síti. Tato věta se tedy používá v lineárních i nelineárních obvodech.
Co je substituční vlastnost?
Substituční vlastnost uvádí, že pokud je proměnná „a“ ekvivalentní jiné proměnné „b“, pak „a“ může být nahrazeno místo „b“ v jakémkoli výrazu nebo rovnici & „b“ může být nahrazeno namísto „ a' v jakémkoli výrazu nebo rovnici.
Tak, to je všechno o přehled střídání věta – obvod s příklady. Zde je pro vás otázka, co je kompenzační teorém?